The ML Validation Playbook: A Primer of Common Validation Techniques
After the AutoML 2025 post-conference presentation of the award-winning paper, “Overtuning in Hyperparameter Optimization” by L. Schneider, B. Bisch, and M. Feurer, I was motivated to discuss it in this blog post. The paper, which received the “Best Paper Award” discusses a phenomenon which the authors call overtuning.
According to the authors, overtuning occurs during hyperparameter optimization (HPO) when a new hyperparameter configuration (HPC) is selected based on its lower validation error, but ultimately leads to a model that performs worse on the unseen test set.
To analyze this effect, the authors reference a wide variety of validation and resampling strategies. Readers who are less familiar with these strategies may find it difficult to fully understanding the paper. Therefore, consider this blog post a primer that gathers all essential validation techniques in one place, and clearly explains them before we discuss the paper itself.
Holdout Validation
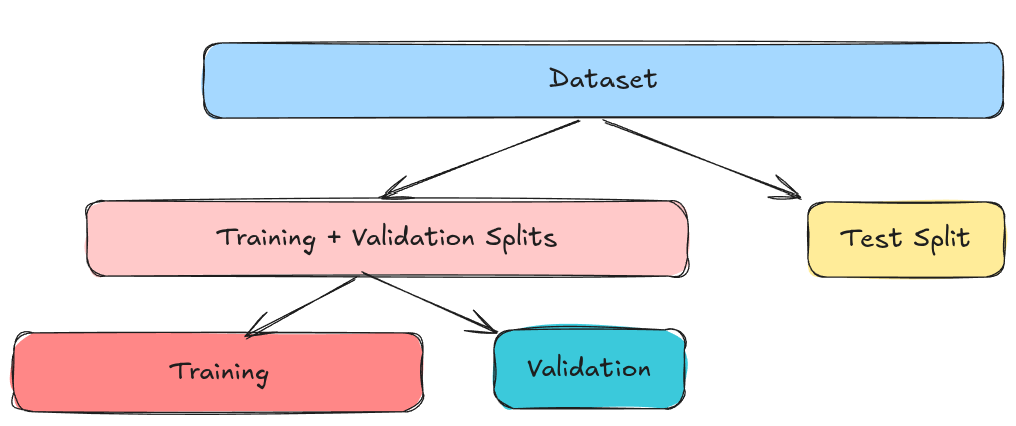
This is probably the simplest validation technique. Suppose you have a dataset and want to perform HPO. First, you split this dataset into a training set and a test set. The test set is kept aside (held out) and is not touched during model training and validation. It is only used once, at the very end, to report the final performance of the model, because using it during training or validation leads to overfitting.
The training set is then divided into two parts: one for training and one for validation. The training set is used to train the model with a specific HP configuration. Then, the validation set is then used to compare HPC configurations.
A working pipeline that uses holdout validation would look something like this:
- Split the dataset into training and test sets, e.g. 80% training, 20% test.
- Split the training set further into training and validation sets, e.g. 80% training, 20% validation.
- Select a HPC.
- Train the model on the training for the selected HPC.
- Evaluate the model on the validation set.
- Repeat this process for all HPCs.
Finally, select the model with the best validation performance, retrain it on the entire training and validation sets, and evaluate it once on the test set, to determine its final generalization performance.
This approach is simple, straightforward, and fast, and it might work well with large datasets. However, it has some drawbacks. Since the generalization performance estimate is based on the data, it may vary depending on which samples end up in the training versus validation splits.
k-Fold Cross-Validation (K-fold CV)
k-Fold Cross-Validation is a more robust validation technique. Starting from a dataset, similarly to holdout validation, we again need a test split which will only be used at the very end to give an estimate of the final generalization performance. Unlike holdout validation, however, we do not just split the remaining data into training and validation.
Instead of a single split, we divide the remaining the data into multiple, smaller k-folds. Then, for a specific HPC, we train the model parameters on the k-1 folds, and estimate the HPC performance on the remaining part of the data. This process is repeated for all folds, and HPCs. The final performance for each HPC is the aggregation (e.g., mean) of the performance on the validation folds.
A working pipeline that uses k-fold CV would look something like this:
- Split the dataset into training and test sets, e.g. 80% training, 20% test.
- Split the training set further into k folds, e.g. k=3 (in practice usually 5 or even 10).
- Select a HPC.
- For each fold:
- Train the model on k-1 folds for the selected HPC.
- Evaluate the model on the remaining fold.
- Aggregate the performance across folds for the selected HPC.
- Repeat these steps for all HPCs.
Once we have selected the best HPC, we retrain the model on the entire training + validation set, and evaluate it once on the test set, to get the final generalization performance.
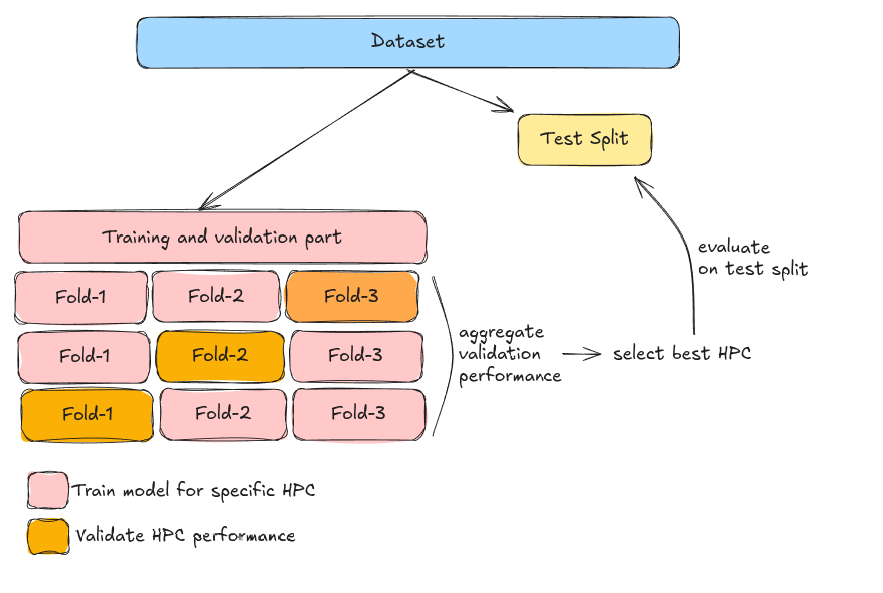
One interesting thing to note here, is that each data point will be used once for validation.
Repeated Holdout & Repeated k-Fold CV
As their name suggests, these techniques are simply repetitions of the two aforementioned validation techniques.
Repeated Holdout
In repeated holdout, we split the data once into two parts, one that will be used for model training and HPC validation and one for estimating generalization performance at the end.
Then, we repeatedly split the training + validation part into training and validation sets, train the model on the training set, evaluate it on the validation set, and aggregate the performance across repetitions for each HPC.
A working pipeline would look like this:
- Split the dataset into training and test sets, e.g. 80% training, 20% test.
- For each outer repetition, in our case 3 times:
- Split the training set further into training and validation sets, e.g. 80% training, 20% validation.
- Select a HPC.
- Train the model on training for the selected HPC.
- Evaluate the model on validation set.
- Repeat these steps for all HPCs.
- Aggregate the performance across the outer repetitions for the selected HPC.
Once we have selected the best HPC, we retrain the model on the entire training + validation set, and evaluate it once on the test set, to get the final generalization performance.
Repeated k-Fold CV
For this method we repeatedly perform k-fold CV. A typical setup for this would be 3x5-fold CV, for which we would perform 5-fold CV three times, each with different folds. A working pipeline would look like this:
- Split the dataset into training and test sets, e.g. 80% training, 20% test.
- For each outer repetition, in our case three times:
- Perform k-fold CV, in our case using k=5.
- Aggregate the performance across outer repetitions for the selected HPC.
Once we have selected the best HPC, we retrain the model on the entire training + validation set, and evaluate it once on the test set, to get the final generalization performance.
Leave-One-Out CV
Leave-one-out CV (LOOCV) is a special case of k-fold CV, where k is equal to the number of data points in the dataset. For each HPC, this means we need to train the model on all but one data point, and evaluate it on the remaining data point. This procedure is then repeated for each data point, and the validation performance for each fold is aggregated to determine the final performance for the specific HPC.
Once we have selected the best HPC, we retrain the model on the entire training + validation set, and evaluate it once on the test set, to get the final generalization performance.
This method may lead to high variance results, and as far as I know, it is rarely used in practice due to its high computational cost for large datasets.
Nested Cross-Validation
This method is also briefly mentioned in the “Overtuning in Hyperparameter Optimization” paper. In nested CV, we essentially replace the outer train + validation / test split with a CV split. This method does not return a single model, since the inner CV loops can produce different best HPCs. Instead, it is particularly useful for assessing HPO strategies, but it does not necessarily produce a single model for deployment, since each outer fold may result in a different optimal HPC.
Note: Parts of the definitions are based on the Applied ML Course by Andreas Mueller.
