Tune My Adam, Please!

Motivation

Adam[1] is still one of the most widely used optimizers in deep learning, and effectively tuning its hyperparameters is key to optimizing performance. However, recent hyperparameter optimization (HPO) approaches typically act as “one-size-fits-all” solutions and lack prior knowledge about the parameters being optimized and their respective effects on learning.

One question that arises is:

Can we do any better if we know that we are optimizing the hyperparameters of Adam, and know what each hyperparameter represents and how it affects training?

In our work “Tune My Adam, Please!” we address this question by modifying an existing HPO framework to specifically target the hyperparameters of the Adam optimizer. The resulting framework outperforms existing approaches on both learning curve extrapolation and HPO from evaluation tasks coming from the TaskSet benchmark, and exhibits strong performance on out-of-distribution tasks.

Contributions

In our work we modified ifBO[2], a recent state-of-the-art framework for in-context Freeze-thaw Bayesian Optimization (BO) Using Freeze-thaw BO[4] allows for stepwise resource allocation instead of training the model being optimized to completion to obtain a new data point for the BO loop.

Additionally,ifBO uses a Prior Data-fitted Network (PFN)[3] as the surrogate model in the BO loop. PFNs are based on the transformer encoder architecture, and are trained once on synthetic data that should closely resemble what the network will encounter in practice. Thus, there is no need for the costly retraining of the surrogate every time a new data point becomes available in the BO loop.

Our main contributions in this work are:

• A drop-in replacement for ifBO’s surrogate model, FT-PFN, with one that is specialized in predicting learning curves of the Adam optimizer, which we call Adam-PFN. Our new surrogate model is still a PFN, so, again, there is no need for retraining. It is also trained from scratch on pre-existing learning curves of the Adam optimizer.
• A new method to augment learning curves which allows us to use a pre-existing set of real learning curves of tasks optimized with the Adam optimizer, and efficiently generate a sufficient number of new curves without to train the transformer-based PFN.

Adam-PFN

Similar to FT-PFN, our new surrogate model, Adam-PFN is trained to predict how learning curves will evolve, given a hyperparameter configuration, and a partial learning curve. One necessary ingredient to specialize our surrogate model to the Adam optimizer, were learning curves of optimization problems using Adam. This is exactly what the TaskSet Benchmark[5] offers.

Real Data: TaskSet Benchmark

TaskSet offers a large collection of diverse tasks optimized using Adam, from language modeling of words, subwords, and characters using RNNs, to text classification, MLPs, and CNNs trained on image data.

The developers of TaskSet focused on different groupings of Adam’s hyperparameters. We chose two of those for our work:

• TaskSet-4P: which include learning rate, \(\beta_1\), \(\beta_2\), and \(\epsilon\)
• TaskSet-8P: which include everything in TaskSet-4P, plus two parameters controlling L1- and L2-regularization, and two parameters that control the learning rate decay schedule.

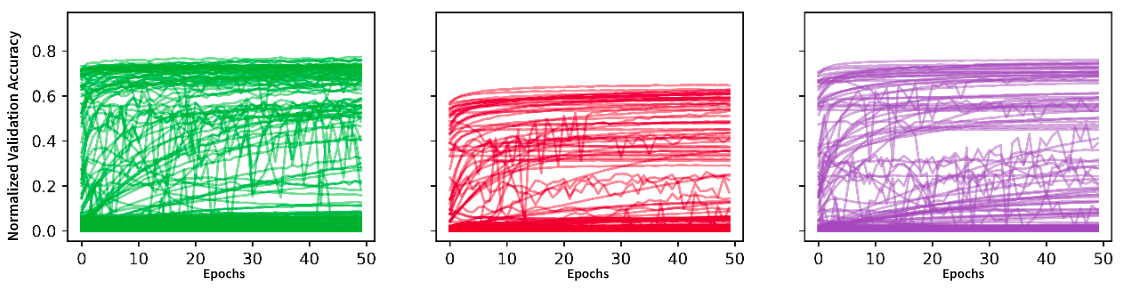
TaskSet’s learning curves were constructed by first sampling 1,000 different hyperparameter configurations for each grouping of Adam’s hyperparameters. Then each optimization task was run for each of the 1,000 different configurations for 10,000 iterations (epochs), keeping track of learning metrics (e.g., training, validation, and test scores) every 200 steps. This means that the resulting learning curves have a length of 50 “epochs”. Figure 1 shows an example of four different sets of learning curves from four randomly sampled tasks from TaskSet.

Figure 1: Learning curves for 1,000 configurations across three different randomly sampled tasks from TaskSet.

Augmentation Method: CDF-augment

To generate an even more diverse set of training tasks we introduce CDF-augment, a local, rank-preserving method for nonlinear tranformation of a tasks “hardness”. Here, by task hardness we mean how difficult a task is, i.e., how quickly or slowly it converges.

Starting from the cumulative distribution function (CDF) of the Beta distribution, we first sample the mean \(\mu\) and concentration \(\kappa\) of the Beta distribution. The mean controls where the Beta distribution is centered, and the concentration controls how clustered the values are around the mean. We sample the mean uniformly at random in the [0, 1] range and the concentration also uniformly at random but on the [2, 5] range.

We then forward-propagate a learning curve \(y\) through the CDF of the resulting Beta distribution as follows:

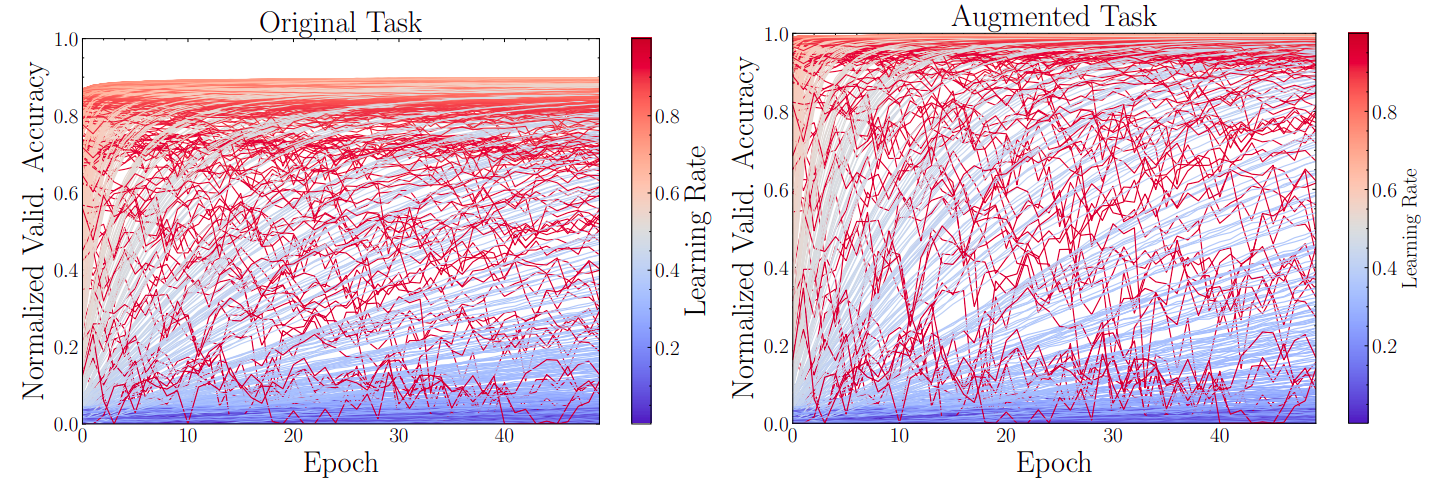
\[y' = F_{Beta}(y; \mu, \kappa)\]

Using this augmentation, we can increase the diversity of the available learning curves as needed, in order to train the data-hungry PFN transformer. Due to the nature of the augmentation, the rank (order) of the learning curves is preserved. Figure 2 shows the result of applying CDF-augment on a set of learning curves. The color of each curve is based on the learning rate value.

Figure 2: (a) A selection of learning curves from TaskSet, the color of each curve is based on the learning rate value. (b) The same set of learning curves augmented with CDF-augment. CDF-augment non-linearly transformed "task hardness" by making the task easier.

Surrogate Model Training

We use the same training pipeline for our surrogate model training as ifBO does for FT-PFN. First, we start with a set of randomly sampled learning curves. We augment and then split each one into a training (context) part and a test (query) part. Our PFN surrogate is then trained to extrapolate the performance of the query points in a curve, using the context points and hyperparameter configuration of that curve.

Experiments

In this brief blog post I will only give a brief description of the results for the 8-parameter case (TaskSet-8P). For a detailed discussion of the results, along with additional ones for the 4-parameter case (TaskSet-4P), check out the full paper.

Evaluation Procedure

We evaluated our surrogate on 12 natural language processing (NLP) tasks from TaskSet that were not used during training, and that are frequently used in prior work.

We assessed the quality of the learning curve extrapolation of our surrogate and its behavior in an HPO setting. For the latter, we used the ifBO framework and replaced the pre-existing FT-PFN surrogate with our own.

In our evaluation, we also included the following two Adam-PFN variants:

• Adam-PFN (No aug.) which was trained on the initial TaskSet tasks without any learning curve augmentation
• Adam-PFN (Mixup) which was trained using the recently introduced Mixup[6] learning curve augmentation method by Lee et al.

Learning Curve Extrapolation Results

To evaluate the quality of the learning curve extrapolation, we follow the same evaluation procedure as ifBO. We pass a batch of learning curves, each observed for a different amount of epochs (some may not be observed at all), and then, for each learning curve and hyperparameter configuration combination, we query the model for its performance at the final epoch. In TaskSet this is epoch 50. We evaluated the learning curve extrapolation performance under different context sizes, which correspond to how many training points are available to the model before extrapolating.

To evaluate the point estimation of a learning curve prediction at the final epoch, we report the Mean Squared Error (MSE) of the prediction. To evaluate the surrogate’s confidence, we report the log-likelihood (LL).

Apart from our Adam-PFN surrogate and its aforementioned variants, we compared against ifBO’s surrogate FT-PFN, DyHPO[8], DPL[7], and a uniform predictor which always output 0.5 for the point estimate (MSE calculation) of the performance at the last epoch, and a uniform distribution for the uncertainty (log-likelihood) calculation.

The results for different context sizes are summarized in Table 1 below.

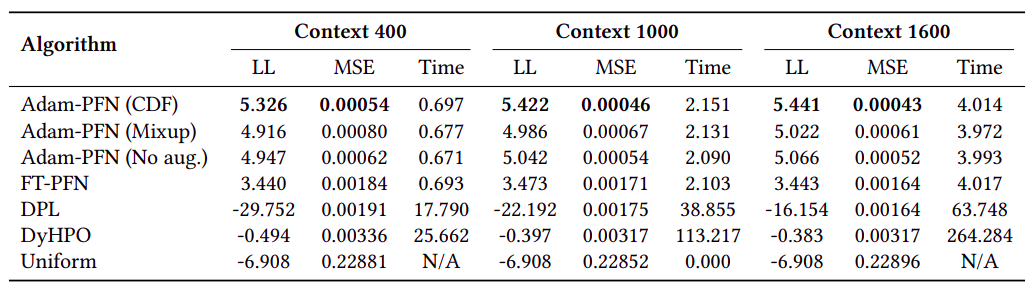
Table 1: Comparison of Adam-PFN (CDF), Adam-PFN (Mixup), Adam-PFN (No Aug.) against the baselines for different context sizes. Values are the median across the 12 evaluation tasks.

Adam-PFN (CDF) outperforms all other baselines and variants both in terms of log-likelihood (LL) and MSE.

HPO

When evaluating the HPO performance of our new surrogate Adam-PFN, we additionally compared against HyperBand[9], ASHA[10], Freeze-thaw with Gaussian Processes[4], and Random Search[11].

Figure 3 shows our HPO results, which include the average normalized regret and the average rank across the 12 evaluation tasks for five different random seeds.

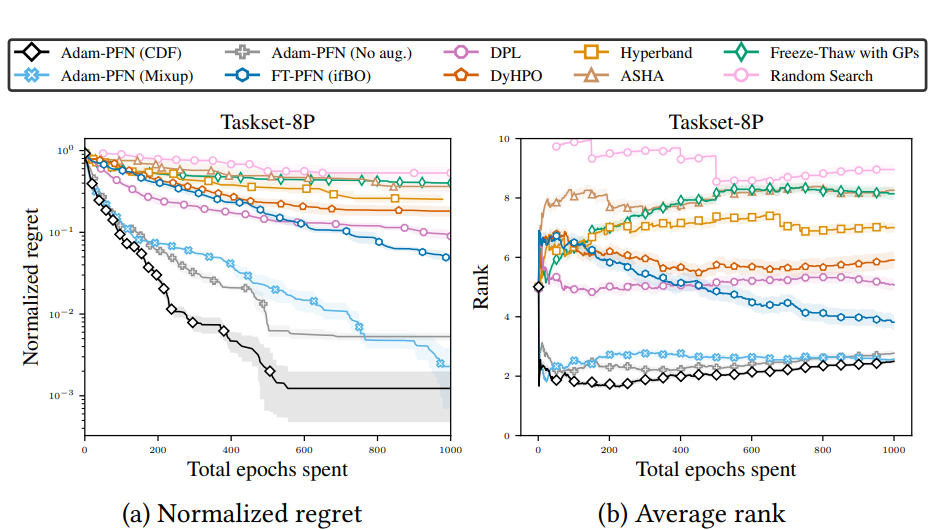
Figure 3: HPO results of normalized regret and average rank of Adam-PFN (CDF) and the two variants Adam-PFN (No aug.), Adam-PFN (Mixup) against the baselines. The results are the mean across the 12 evaluation tasks for five different random seeds.

Adam-PFN (CDF) outperforms all baselines, both in terms of normalized regret and average rank. The other two variants Adam-PFN (No aug.) and Adam-PFN (Mixup) perform similarly well.

Evaluation In The Wild: Out-Of-Distribution Tasks

Finally, we evaluate the HPO performance of all Adam-PFN variants on some real-world tasks from the publicly available PyTorch Examples.

For this evaluation, we only compare against HyperBand, ASHA, ifBO (FT-PFN), and Random Search. The results are presented in Figure 4.

Figure 4: HPO results of normalized regret and average rank of Adam-PFN (CDF) and the two variants Adam-PFN (No aug.), Adam-PFN (Mixup) against the baselines, on Out-Of-Distribution tasks. The results are the mean across tasks for five random seeds.

Based on the results, Adam-PFN (CDF) appears to perform best early on, on average. As the budget increases, however, FT-PFN catches up and eventually surpasses our model. An approach that warm-starts the HPO process on out-of-distribution tasks with Adam-PFN (CDF) and then switches to FT-PFN might be the optimal approach in these cases, but we leave that for future work.

Limitations and Future Work

We believe our work highlights the importance of specialization and the use of prior knowledge in HPO. However, we acknowledge that our surrogate is trained and tested on a fixed search space with a predetermined number of hyperparameters. One possible direction for future work, is to generalize the model for different sets of HPs.

Finally, especially based on our results on out-of-distribution tasks, it might be worth exploring how our prior could be mixed with the one used in ifBO.

Conclusion

That’s all I wanted to share in this short blog post. I hope you enjoyed it!

Be sure to check out the full paper for a more detailed discussion of the results, the surrogate model architectures, the tasks we used during training, limitations and future work directions, as well as a detailed description of baselines and related work.

References

1. Adam: A Method for Stochastic Optimization , Kingma, D. P. and J. Ba, 3rd International Conference on Learning Representations , 2015
2. In-Context Freeze-Thaw Bayesian Optimization for Hyperparameter Optimization, Rakotoarison, H. et al. 41st International Conference on Machine Learning , 2024
3. Transformers Can Do Bayesian Inference, Müller, S. et al. International Conference on Learning Representations , 2022
4. Freeze-Thaw Bayesian Optimization, Swersky, K., J. Snoek, and R. P. Adams, 2014
5. Using a thousand optimization tasks to learn hyperparameter search strategies, Metz, L. et al. International Conference on Learning Representations , 2020
6. Cost-Sensitive Multi-Fidelity Bayesian Optimization with Transfer of Learning Curve Extrapolation, Lee, D. B. et al., 2024
7. Scaling Laws for Hyperparameter Optimization, Kadra, A. et al, 37th Conference on Neural Information Processing Systems , 2023
8. Supervising the Multi-Fidelity Race of Hyperparameter Configurations, Wistuba, M., A. Kadra, and J. Grabocka, 36th Conference on Neural Information Processing Systems , 2022
9. Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization, Li, L., K. Jamieson, G. DeSalvo, et al, Journal of Machine Learning Research, , 2018
10. A System for Massively Parallel Hyperparameter Tuning, Li, L., K. Jamieson, A. Rostamizadeh, et al., Proceedings of Machine Learning and Systems, 2020
11. Random Search for Hyper-Parameter Optimization , Bergstra, J. and Bengio, Y, Journal of Machine Learning Research , 2012